One type of noise generation that I haven't seen discussed much is the Diamond-Square algorithm which is an extension of the Mid-point Displacement algorithm, hence the reason for writing this. This type of algorithm in my opinion generates very natural looking noise which is suitable for terrain generation and it can also be used to generate detail on existing height-maps with realistic results without much effort. I will jump straight into it.
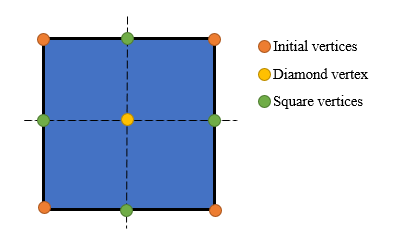
The essence of the algorithm is division and displacement at the point of division. You start with a square and split it in the middle both vertically and horizontally, doing this yields 5 new points. Once the new points are obtained height is sampled from the points around the new point and a random offset is added, this sampling is done in two steps, a Diamond step from which the center point derives its new displacement and a square step that derives the height of the other four points. Diamond step is first simply because the Square step requires the newly acquired height.
Looking at the above image showing the first Diamond step, we have derived the central point by averaging the existing four points and adding an offset R which is multiplied by the Current depth multiplier c. Essentially your c starts at 1.0f and you half it after you have finished one level of subdivision process, which is a Diamond and Square pass. The R value is a random number that has the range that you want to bind your displacement to, for instance if you wish to have terrain that spans from -4f to 4f your need a function which will return a random number R that has a range of -4f to 4f, any range can be used. I have found that using same lower and upper bounds for the range with the lower bound being negative and upper bound positive produces the best results.
In the image above is the first Square step, we need to work out the n1-4 displacements and this is done by taking the points that are adjacent horizontally and vertically to the point that we wish to evaluate. There is a little trick when dealing with the border points and in the first Square step all of the new points are border points. We are missing a value which I have designated X above, there are two ways to solve this. Simple solution is to make X = C, the more interesting approach is to make X=n3 when working out n1, X=n4 when working out n2 and so on. Problem there is that if you are working out n1 and need n3, n3 needs n1, to solve this I pass n3 all the values that n1 is using and use that to calculate the averaged midpoint before adding the offset, the new n3 value is then used to set n1 = n3. This method produces wrapping of the noise/height map on all four sides.
The above two steps are repeated until you have reached the level of detail that you desire. And that might even be enough to get you going, but there are some details that are essential for producing height-maps without artifacts, have a look at the mapping below as we head into the third level of detail. Initial points are Orange, first level pass is Green, second level pass is Yellow, Red is the Diamond step of the third level and Purple is the Square step of the third level.
It's pretty obvious that our new Red and Purple points are dependent on both their level and the levels above them for their midpoint average calculation, if we don't at least nudge the calculation in the right direction, artifacts appear, they manifest as small dimples in the height-map that are more pronounced if you make a 3D model out of the data. During the Square step (the easier one to correct) the level of adjacent points depends on the x value of the position you are evaluating, if x%2=0 the top and bottom values are of previous level and if x%2=1, left and right are of the previous level. It's a bit more complicated for the Diamond step I won't go into detail and will rather post the code below, but the level is dependent on both the x and y position of the point being evaluated.
float hlt = data[x, y];
float hrt = data[x + 1, y];
float hlb = data[x, y + 1];
float hrb = data[x + 1, y + 1];
float add = 0f;
if (y % 2 == 0)
if (x % 2 == 0) { add += hrb + hlt; } else { add += hlb + hrt; }
else
if (x % 2 == 0) { add += hrt + hlb; } else { add += hlt + hrb; }
float mid = (hlt + hrt + hlb + hrb + add) / 6.0f;
float offset = (this.rand.GetHeight() * this.cDeviance);The resulting formula doubles the values of the the heights that were a level above and averages them over 6 points instead of 4, this is true of the Square step adjustment too.
The beauty of this algorithm is that you can take a map of any resolution and increase that resolution believably by only having to adjust the R range and if you need to, the seed for the function that returns R. I think that's about it, a C# Unity implementation link is below, hope you find this useful.
https://pastebin.com/Bm4nscyE